3. Trigonometry
f. Applications of Trig Functions
2. Solving Triangles
To Solve a Triangle means to find the lengths of
all the sides and the measure of all the angles given some of them.
An SAS Triangle is a triangle for which we know
\(2\) sides and the angle between them.
An ASA Triangle is a triangle for which we know
\(2\) angles and the side between them.
An SSS Triangle is a triangle for which we know
all \(3\) sides.
An ASS Triangle is a triangle for which we know
\(2\) sides and an angle that is not between them.
Solving a triangle is usually accomplished using the Law of Sines and the Law of Cosines and the sum of the angles is \(180^\circ\). We will demonstrate this using examples and exercises.
You will need a calculator to do these problems. Be sure to set the calculator to use degrees or remember to convert from radians to degrees by multiplying by \(\dfrac{180^\circ}{\pi}\). Keep answers to \(2\) decimal places.
Solving SAS Triangles
A triangle \(\triangle ABC\) has two sides of length of \(a=4\,\text{in}\) and \(b=5\,\text{in}\). The angle between them is \(C=45^\circ\). Find the length of the third side and the other two angles.
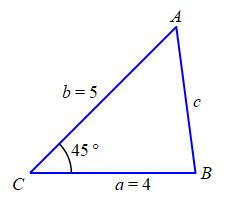
By the Law of Cosines, the third side, \(c\), satisfies: \[\begin{aligned} c^2&=a^2+b^2-2ab\cos C \\ &=4^2+5^2-2\cdot4\cdot5\cos45^\circ \\ &=41-20\sqrt{2} \\ c&=\sqrt{41-20\sqrt{2}}\approx3.566 \end{aligned}\] The other two angles can be found using either the Law of Sines or the Law of Cosines. We'll use the Law of Sines. Given \(a\), \(b\), \(c\) and \(C\), the angles \(A\) and \(B\) satisfy: \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \]
So: \[\begin{aligned} \sin A&=a\dfrac{\sin C}{c}=4\dfrac{\sin45^\circ}{3.566}\approx0.793 \\ A&\approx52.48^\circ \\ \sin B&=b\dfrac{\sin C}{c}=5\dfrac{\sin45^\circ}{3.566}\approx0.9915 \\ B&\approx82.52^\circ \end{aligned}\]
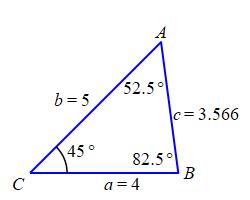
We check by adding up the angles: \[ 45^\circ+52.48^\circ+82.52^\circ=180^\circ \]
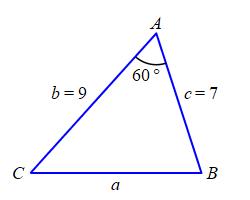
A triangle \(\triangle ABC\) has two sides of length of \(b=9\,\text{in}\) and \(c=7\,\text{in}\). The angle between them is \(A=60^\circ\). Find the length of the third side and the other two angles.
\(a = 8.185\,\text{in}\), \(B = 72.22^\circ\), \(C = 47.79^\circ\)
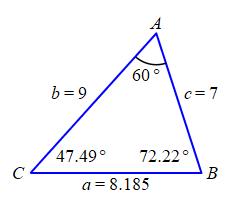
By the Law of Cosines, the third side, \(a\), satisfies: \[\begin{aligned} a^2&=b^2+c^2-2bc\cos A \\ &=9^2+7^2-2\cdot9\cdot7\cos60^\circ \\ &=130-63=67 \\ a&=\sqrt{67}\approx8.185 \end{aligned}\] By the Law of Sines, the angles \(B\) and \(C\) satisfy: \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \] Since \(c\) is not the longest side, its opposite angle must be acute. So: \[\begin{aligned} \sin C&=c\dfrac{\sin A}{a}=7\dfrac{\sin60^\circ}{8.185}\approx0.7406 \\ C&=\arcsin90.74\approx47.79^\circ \end{aligned}\] Since \(b\) is the longest side, its opposite angle might be acute or obtuse. So: \[\begin{aligned} \sin B&=b\dfrac{\sin A}{a}=9\dfrac{\sin60^\circ}{8.185}\approx0.952 \\ B&=\arcsin(0.952)\approx72.22^\circ \quad \text{or} \\ B&=108^\circ-\arcsin(0.952)\approx107.78^\circ\\ \end{aligned}\] To find which \(B\) is correct, we check the sum of angles is \(180^\circ\). First for the acute \(B\): \[ 60^\circ+72.22^\circ+47.79^\circ\approx180.01^\circ \] Since this is \(180^\circ\) within rounding error, \(B=72.22^\circ\). We don't need to check the obtuse angle. See the answer for a plot.
tc
A triangle \(\triangle ABC\) has two sides of length of \(a=2\,\text{in}\) and \(c=5\,\text{in}\). The angle between them is \(B=30^\circ\). Find the length of the third side and the other two angles.
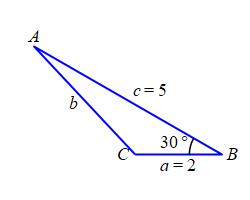
\(b = 3.418\,\text{in}\), \(A = 17.01^\circ\), \(C = 133^\circ\)
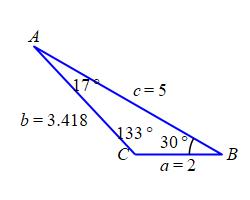
By the Law of Cosines, the third side, \(b\), satisfies: \[\begin{aligned} b^2&=a^2+c^2-2ac\cos B \\ &=2^2+5^2-2\cdot2\cdot5\cos30^\circ \\ &=29-10\sqrt{3}\approx11.68 \\ b&=\sqrt{11.68}\approx3.418 \end{aligned}\] By the Law of Sines, the anglea \(A\) and \(C\) satisfy: \[ \dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c} \] So: \[\begin{aligned} \sin A&=a\dfrac{\sin B}{b}=2\dfrac{\sin30^\circ}{3.418}\approx0.2926 \\ A&=\arcsin(0.929)\approx17.01^\circ \\ \sin C&=c\dfrac{\sin B}{b}=5\dfrac{\sin30^\circ}{3.418}\approx0.7314 \\ C&=\arcsin(0.7314)\approx47.0^\circ \quad \text{or} \quad 180^\circ-47.0^\circ=133.0^\circ \end{aligned}\] To find which \(C\) is correct, we check the sum of angles is \(180^\circ\). First for the acute \(C\): \[ 30^\circ+17.01^\circ+47.0^\circ\approx94.01^\circ \] Since this does not work, we check the obtuse \(C\): \[ 30^\circ+17.01^\circ+133.0^\circ\approx180.01^\circ \] Since this works, \(C=133.0^\circ\).
tc
Solving ASA Triangles
A triangle \(\triangle ABC\) has two angles of \(A=45^\circ\) and \(B=60^\circ\). The side between them has length \(c=4\,\text{in}\). Find the third angle and the lengths of the other \(2\) sides.
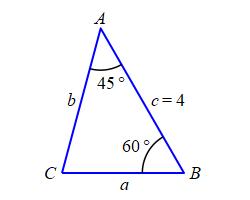
The third angle is found by subtracting from \(180^\circ\): \[ C=180^\circ-A-B=180^\circ-45^\circ-60^\circ=75^\circ \] The other \(2\) sides can be found using either the Law of Sines or the Law of Cosines. We'll use the Law of Sines. The sides \(a\) and \(b\) satisfy:
\[ \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C} \] So: \[\begin{aligned} a&=c\dfrac{\sin A}{\sin C}=4\dfrac{\sin45^\circ}{\sin75^\circ}\approx2.928 \\ b&=c\dfrac{\sin B}{\sin C}=4\dfrac{\sin60^\circ}{\sin75^\circ}\approx3.586 \end{aligned}\]
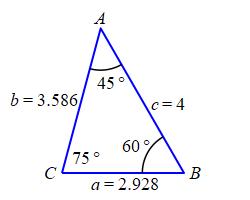
We check using the Law of Cosines: \[\begin{aligned} c&=\sqrt{a^2+b^2-2ab\cos C} \\ &=\sqrt{2.928^2+3.586^2-2\cdot2.928\cdot3.586\cos75^\circ} \\ &\approx3.9997 \end{aligned}\] which is \(4\) except for calculator error.
A triangle \(\triangle ABC\) has two angles of \(A=15^\circ\) and \(C=30^\circ\). The side between them has length \(b=7\,\text{in}\). Find the third angle and the lengths of the other \(2\) sides.
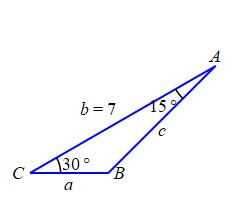
\(B = 135^\circ\), \(a = 2.562\,\text{in}\), \(c = 4.950\,\text{in}\)
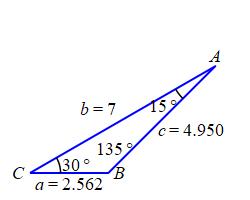
The third angle is found by subtracting from \(180^\circ\): \[ B=180^\circ-A-C=180^\circ-15^\circ-30^\circ=135^\circ \] The other \(2\) sides can be found using either the Law of Sines or the Law of Cosines. We'll use the Law of Sines. The sides \(a\) and \(b\) satisfy: \[ \dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C} \] So: \[\begin{aligned} a&=b\dfrac{\sin A}{\sin B}=7\dfrac{\sin15^\circ}{\sin135^\circ}\approx2.562 \\ c&=b\dfrac{\sin C}{\sin B}=7\dfrac{\sin30^\circ}{\sin135^\circ}\approx4.950 \end{aligned}\]
tc
We check using the Law of Cosines: \[\begin{aligned} b&=\sqrt{a^2+c^2-2ac\cos B} \\ &=\sqrt{2.562^2+4.950^2-2\cdot2.562\cdot4.950\cos135^\circ} \\ &\approx7 \end{aligned}\]
Solving SSS Triangles
A triangle \(\triangle ABC\) has sides \(a=4\,\text{m}\), \(b=5\,\text{m}\), and \(c=6\,\text{m}\). Find the \(3\) angles.
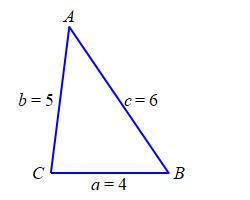
We will use the Law of Cosines to find the \(3\) angles:
\[\begin{aligned} \cos A&=\dfrac{b^2+c^2-a^2}{2bc} \\ &=\dfrac{5^2+6^2-4^2}{2\cdot5\cdot6}=\dfrac{3}{4} \\ A&=\arccos\dfrac{3}{4}\approx41.41^\circ \\ \cos B&=\dfrac{c^2+a^2-b^2}{2ca} \\ &=\dfrac{6^2+4^2-5^2}{2\cdot6\cdot4}=\dfrac{9}{16} \\ B&=\arccos\dfrac{9}{16}\approx55.77^\circ \\ \cos C&=\dfrac{a^2+b^2-c^2}{2ab} \\ &=\dfrac{4^2+5^2-6^2}{2\cdot4\cdot5}=\dfrac{1}{8} \\ C&=\arccos\dfrac{1}{8}\approx82.82^\circ \\ \end{aligned}\]

We check by adding up the angles: \[ 41.41^\circ+55.77^\circ+82.82^\circ=180^\circ \]
A triangle \(\triangle ABC\) has sides \(a=5\,\text{m}\), \(b=9\,\text{m}\), and \(c=12\,\text{m}\). Find the \(3\) angles.
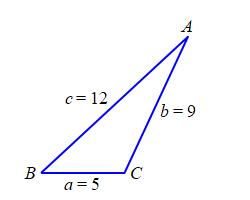
\(A = 22.19^\circ\), \(B = 42.83^\circ\), \(C = 114.97^\circ\)
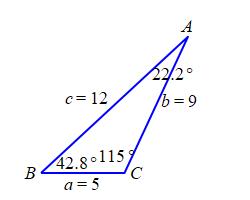
We will use the Law of Cosines to find the \(3\) angles: \[\begin{aligned} \cos A&=\dfrac{b^2+c^2-a^2}{2bc} \\ &=\dfrac{9^2+12^2-5^2}{2\cdot9\cdot12}=\dfrac{200}{216} \\ A&=\arccos\dfrac{25}{27}\approx22.19^\circ \\ \cos B&=\dfrac{c^2+a^2-b^2}{2ca} \\ &=\dfrac{12^2+5^2-9^2}{2\cdot12\cdot5}=\dfrac{88}{120} \\ B&=\arccos\dfrac{11}{15}\approx42.83^\circ \\ \cos C&=\dfrac{a^2+b^2-c^2}{2ab} \\ &=\dfrac{5^2+9^2-6^2}{2\cdot5\cdot9}=\dfrac{-38}{90} \\ C&=\arccos\dfrac{-19}{45}\approx114.97^\circ \\ \end{aligned}\]
tc
We check by adding up the angles: \[ 22.19^\circ+42.83^\circ+114.97^\circ\approx180^\circ \]
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum